Step-by-step explanation:
We can represent the situation with the following figure
Therefore, we need to calculate the magnitude of F1 and F2.
The magnitude of electric force between two charges is equal to
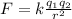
Where k = 8.98 x 10^9, q1 and q2 are the charges and r is the distance between the charges. The distance between the object of charge -4 x 10^(-3) C and the object of charge +1C can be calculated using the Pythagorean theorem as

Therefore, the distance between the charges is 70.71 m.
Then, replacing q1 = -4 x 10^(-3) C, q2 = +1C and r = 70.71 m, on the initial equation, we get:
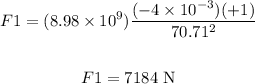
To calculate F2, we need to replace q1 = +2 x 10^(-3) C, q2 = +1C, and r = 50 m, so
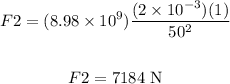
Now, we need to calculate the resultant force, so we need to identify the x and y coordinates of each force and add them
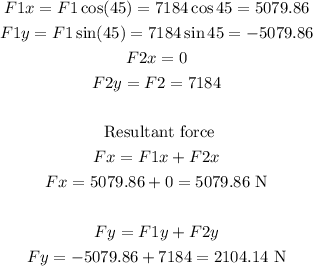
Finally, we can calculate the magnitude and direction of the force as follows
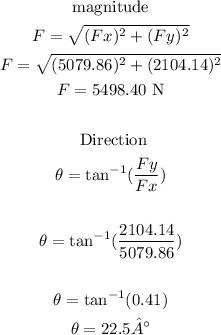
Therefore, the magnitude of the electric force is 5498.40 N and the direction is 22.5 degrees.