Because the triangles have same angles, we can use the relation:
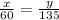
And from this we have the relation:
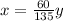
The area of this triangles are measured as half of the producr of the basis with the height.
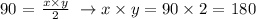
Now we have two equations with two uknown values. We can just substitute the value of x from the first into the second. Than we get:
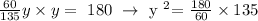
![y^2=\text{ 405 }\rightarrow\text{ y = }\sqrt[]{405}\text{ = }\sqrt[\square]{9^2^{}*5}\text{ = }9*\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/axz82dmdpzyszd3vophtu6q4m06qb70mpk.png)
From this, we can substitute in the second relation that we got:
![x* y=180\text{ }\rightarrow\text{ x}*9*\sqrt[]{5\text{ }}=180](https://img.qammunity.org/2023/formulas/mathematics/college/v348qoaws8itc4yr1juwaciqaddi5rwgjc.png)
![x=\frac{180}{9*\sqrt[]{5}}=\frac{20}{\sqrt[\square]{5}}=\frac{20*\sqrt[]{5}}{\sqrt[]{5}*\sqrt[]{5}}=\frac{20*\sqrt[]{5}}{5}=4*\sqrt[]{5}cm](https://img.qammunity.org/2023/formulas/mathematics/college/de0gmlubxwyxatstcohxr43bprj98renxe.png)
From this, we got:
![x\text{ = 4}*\sqrt[]{5}\text{ cm}](https://img.qammunity.org/2023/formulas/mathematics/college/anzsrfu6exa5ym1wfxkyhxc7riwcqrg6jz.png)
and
![\text{y = }9*\sqrt[]{5}\text{ cm}](https://img.qammunity.org/2023/formulas/mathematics/college/3kfl5362foe26kwbn9vbe23javnld48646.png)