Question

Find the values of x and y when the smaller triangle has an area of 90 cm2.cm.The value of x is cm and the value of y is(Type exact answers, using radicals as needed. Rationalize all denominators.)

Answer 1

Because the triangles have same angles, we can use the relation:

`(x)/(60)=(y)/(135)`

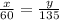
And from this we have the relation:

`x=(60)/(135)y`

The area of this triangles are measured as half of the producr of the basis with the height.

`90\text{ = }(x* y)/(2)\text{ }\rightarrow x* y=90*2\text{ = 180}`

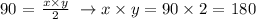
Now we have two equations with two uknown values. We can just substitute the value of x from the first into the second. Than we get:

`(60)/(135)y* y=\text{ 180 }\rightarrow\text{ y }^2\text{= }(180)/(60)*135`
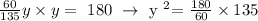
`y^2=\text{ 405 }\rightarrow\text{ y = }\sqrt[]{405}\text{ = }\sqrt[\square]{9^2^{}*5}\text{ = }9*\sqrt[]{5}`

From this, we can substitute in the second relation that we got:

`x* y=180\text{ }\rightarrow\text{ x}*9*\sqrt[]{5\text{ }}=180`
`x=\frac{180}{9*\sqrt[]{5}}=\frac{20}{\sqrt[\square]{5}}=\frac{20*\sqrt[]{5}}{\sqrt[]{5}*\sqrt[]{5}}=\frac{20*\sqrt[]{5}}{5}=4*\sqrt[]{5}cm`

From this, we got:

`x\text{ = 4}*\sqrt[]{5}\text{ cm}`

and

`\text{y = }9*\sqrt[]{5}\text{ cm}`