Question

In the circle above, the measure of arc VXY is 320 degrees. The measure of angle VXY is ___ degrees.

Answer 1

Given, the measure of arc VXY= 320 degrees.

Since the sum of the major and minor arcs of a circle is 360 degrees, we can write

`\begin{gathered} m(\text{arc VY)+}m(arc\text{ VXY})\text{=}360^(\circ) \\ m(\text{arc VY)=}360^(\circ)-m(arc\text{ VXY}) \\ \text{=}360^(\circ)-320^(\circ) \\ =^{}40^(\circ) \end{gathered}`

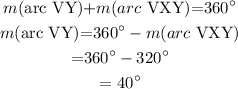
If an angle is inscribed in a circle, then the angle equals one half the measure of its intercepted arc.

Arc VY is the intercepted arc of

Hence,
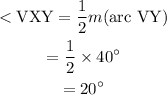`\begin{gathered} <\text{VXY}=(1)/(2)m(\text{arc VY)} \\ =(1)/(2)*40^(\circ) \\ =20^(\circ) \end{gathered}`Therefore, the measure of angle VXY is 20 degrees.