Question

Find line DFFind measure of Angle D Find measure of Angle E

Answer 1

Since it is a right triangle then you can use the Pythagorean theorem to find the measure of the segment DF, like this

`\begin{gathered} a^2+b^2=c^2 \\ \text{ Where a, b are the legs and c is the hypotenuse} \end{gathered}`

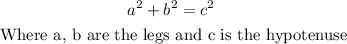
In this case, you have

`\begin{gathered} a=DF \\ b=FE=19 \\ c=DE=28 \end{gathered}`
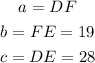
`\begin{gathered} a^2+b^2=c^2 \\ a^2+(19)^2=(28)^2 \\ \text{ Subtract (19)}^2\text{ on both sides of the equation} \\ a^2+(19)^2-(19)^2=(28)^2-(19)^2 \\ a^2=(28)^2-(19)^2 \\ \text{Apply square root on both sides of the equation} \\ \sqrt[]{a^2}=\sqrt[]{(28)^2-(19)^2} \\ a=20.57 \end{gathered}`

Now to find the measure of angle D, you can use the trigonometric ratio

`\sin (\theta)=\frac{\text{opposite leg }}{\text{hypotenuse}}`

In this case, you have

`\begin{gathered} \sin (D)=(19)/(28) \\ \text{ Apply the inverse function of sin(}\theta\text{) } \\ \sin ^(-1)(\sin (D))=\sin ^(-1)((19)/(28)) \\ D=\sin ^(-1)((19)/(28)) \\ D=42.7\text{ \degree} \end{gathered}`

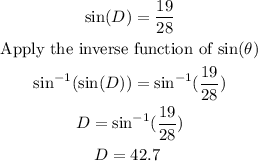
Finally, to find the measure of angle E, you can use the trigonometric ratio

`\cos (\theta)=\frac{\text{ adjacent leg}}{hypotenuse}`

In this case, you have

`\begin{gathered} \cos (E)=(19)/(28) \\ \text{ Apply the inverse function of cos(}\theta\text{)} \\ \cos ^(-1)(\cos (E))=\cos ^(-1)((19)/(28)) \\ E=\cos ^(-1)((19)/(28)) \\ E=47.3\text{ \degree} \end{gathered}`

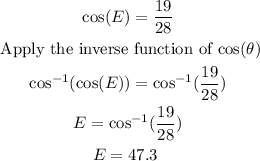
Therefore,

*The measure of the segment DF is 20.57.

*The measure of angle D is 42.7°.

*The measure of angle E is 47.3.