Given a torque-time graph.
The angular impulse can be calculated as the product of the torque and the time. The angular impulse can be found from a torque-time graph by calculating the area under the curve just like we calculate impulse from a force-time graph.
The area under the curve in the interval 1.0 s to 1.5 s forms a triangle.
From the graphy, the approximate height of the triangle is h=10 Nm
The approximate base of the triangle is b=1.5-1.0=0.5 s
The area of a triangle is given by,
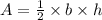
On substituting the known values,
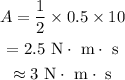
Thus the approximate angular impulse provided by the engine is 3 N·m·s
Therefore the correct answer is option 5.