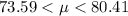Given that:
- You measure 50 textbooks' weights.
- They have a Mean of 77 ounces.
- The Population Standard Deviation is 12.3 ounces.
You need to use the following formula:
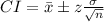
Where:
- The Sample Mean is:
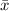
- The z-value for the corresponding Confidence Interval Level is "z".
- The Sample Standard Deviation is σ.
- The Sample Size is "n".
In this case:
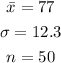
By definition, for a 95% Confidence Interval:
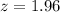
Then, by substituting values and evaluating, you get these two values:
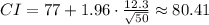
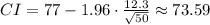
Hence, the answer is: