Question

You measure 50 textbooks' weights, and find they have a mean weight of 77 ounces. Assume the population standard deviation is 12.3 ounces. Based on this, construct a 95% confidence interval for the true population mean textbook weight.Give your answers as decimals, to two places < μ<

Answer 1

Given that:

- You measure 50 textbooks' weights.

- They have a Mean of 77 ounces.

- The Population Standard Deviation is 12.3 ounces.

You need to use the following formula:

`CI=\bar{x}\pm z(\sigma)/(√(n))`

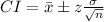
Where:

- The Sample Mean is:

`\bar{x}`

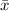
- The z-value for the corresponding Confidence Interval Level is "z".

- The Sample Standard Deviation is σ.

- The Sample Size is "n".

In this case:

`\begin{gathered} \bar{x}=77 \\ \sigma=12.3 \\ n=50 \end{gathered}`

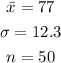
By definition, for a 95% Confidence Interval:

`z=1.96`

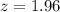
Then, by substituting values and evaluating, you get these two values:

`CI=77+1.96\cdot(12.3)/(√(50))\approx80.41`

`CI=77-1.96\cdot(12.3)/(√(50))\approx73.59`

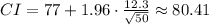
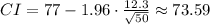
Hence, the answer is:

`73.59<\mu<80.41`