Question

The UN's measures gender equality. The mean number of hours spent on household chores is another measure of gender equality for a nation. Suppose that a UN study aims to estimate the mean hours spent on household chores by adults 15 years and older for a particular country within 0.2 hour. The desired level of confidence is 96%. From the previous studies, the the population standard deviation is 0.8 hours.What is the necessary sample size to achieve the above margin of error?

Answer 1

We have to find the minimum sample size.

The margin of error that it is aimed is ±0.2 hours from the real mean.

The population standard deviation is 0.8 hours.

The desired level of confidence is 96%. This corresponds to a z-score of 2.054.

We can relate sample size with the given information as:

`\begin{gathered} e=(\sigma)/(√(n))\cdot z \\ √(n)=(\sigma)/(e)\cdot z \\ n=((\sigma\cdot z)/(e))^2 \end{gathered}`

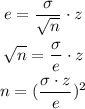
If we replace e = 0.2, σ = 0.8 and z = 2.054 we can calculate the sample size n as:

`\begin{gathered} n=((0.8*2.054)/(0.2))^2 \\ \\ n=(8.216)^2 \\ n\approx67.5 \\ n\approx68 \end{gathered}`

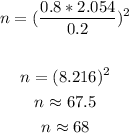
Answer: the sample size has to be at least 68 people.

W