Question

Two airplanes leave an airport at the same time and travel in opposite directions. One plane travels 81km/h faster than the other. If the two planes are 5499 kilometers apart after 3 hours, what is the rate of each plane?

Answer 1

Rember that we define velocity as distance over time

`v=(d)/(t)`

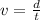
Solving for d,

`v=(d)/(t)\rightarrow vt=d`

We can define distance as the product between velocity and time.

Now, let x be velocity of plane A and x + 81 ve the velocity of plane B

We can establish that the distance between both planes is the sum of the distances they both have traveled.

`D=d_A+d_B`

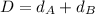
Using the definition for distance we've established from the start,

`\begin{gathered} D=v_At+v_Bt \\ \rightarrow D=xt+(x+81)t \end{gathered}`

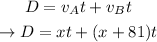
Now, we know that after 3 hours, they are 5499 km apart. This way,

`5499=x\cdot3+(x+81)\cdot3`

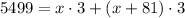
Solving for x,

`\begin{gathered} 5499=x\cdot3+(x+81)\cdot3 \\ \rightarrow5499=3x+3x+243 \\ \rightarrow5256=6x \\ \rightarrow x=(5256)/(6) \\ \\ \Rightarrow x=876 \end{gathered}`

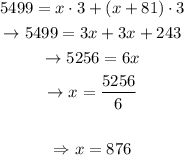
This way,

`\begin{gathered} v_A=x\rightarrow v_A=876 \\ v_B=x+81\rightarrow v_B=957 \end{gathered}`

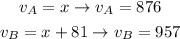
We can conclude that one plain is traveling at 876 Km/h and the other one travels at 957 Km/h