In this problem, we have the following data sample:
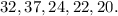
We must compute the standard deviation of this data sample.
1) First, we compute the mean value which is given by the following formula:
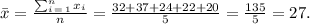
2) Now, we compute the standard deviation using the following formula:
![\sigma=\sqrt[]{\frac{\sum^n_{i\mathop{=}1}(x_i-\bar{x})^2}{n-1}}=\sqrt[]{(208)/(5-1)}\cong7.21.](https://img.qammunity.org/2023/formulas/mathematics/college/9f403nvksztdtd1jadi4bxyq6ti9bz7hvz.png)
Answer
The standard deviation is 7.21.