we have the functions
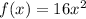
![g(x)=(1)/(4)\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/huhz4uwq0kz2ubny6n5td6n29qy258lv71.png)
step 1
Find f(g(x))
![f(g(x))=16((1)/(4)\sqrt[]{x})^2](https://img.qammunity.org/2023/formulas/mathematics/college/rydjupsy8chw3m74yvj458fg6ri6nnv13n.png)
simplify

therefore
Part 1
If x≥0 the value of f(g(x)) is x
step 2
Find g(f(x))
![g(f(x))=(1)/(4)\sqrt[\square]{16x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/vl9c8bflofulg5aifyoo0cyzqh60em4e0f.png)
simplify
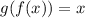
therefore
Part 2
If x≥0 the value of g(f(x)) is the same as the first
step 3
Find the inverse of function f(x)
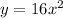
exchange the variables

isolate the variable y
![\begin{gathered} y^2=(x)/(16) \\ y=\pm(1)/(4)\sqrt[\square]{x} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aynjtppkyrk8ynq9t369ce1qg28xidzfcf.png)
Part 3
the functions f(x) and g(x) are inverse functions