1. the sequence is:
500, 250, 125, ...
the common ratio (r) is:
250/500 = 1/2 = 0.5
125/250 = 1/2 = 0.5
So, the sequence is a geometric sequence.
Explicit formula:
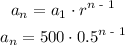
Recursive formula:
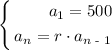
2. In the formulas, n represents days. Using the explicit formula with an = 1, we get:
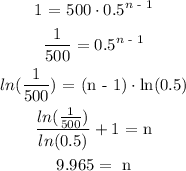
then, after 10 days there will be less than 1 skittle in the bag