Answer:
151.93 bushels
Step-by-step explanation:
First, let's find the volume of the truncated cone using the following equation
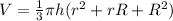
Where h is the height of the cone, r is the smallest radio and R is the largest radio. So, replacing h = 4 ft, r = 1.5 ft and R = 4.5 ft, we get:
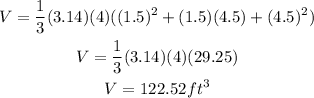
Because the radius is half the diameter, so r = 3ft/2 = 1.5 ft and R = 9ft/2 = 4.5 ft.
Now, we know the volume in cubic feet. To find the volume in bushels, we will use the conversion factor 1 ft³ = 1.24 bushels.
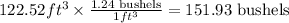
Therefore, the answer is 151.93 bushels