Question

A massive light hangs over the table in Jeremy's dining room. The light is supported by four strong chains which make an angle of 73.9° with the horizontal. The force in each chain is 38.4 N. Determine the mass of the light in kilograms (kg). Use the approximation g ≈ 10 m/s^2.Answer: ___________ kg

Answer 1

Given:

The is supported by four strong chains which make an angle of

`\theta=73.9\degree`

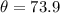
The force on each chain is

`F=38.4\text{ N}`

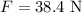
The acceleration due to gravity is

`g=10\text{ m/s}^2`

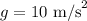
To find:

The mass of the light

Step-by-step explanation:

The horizontal force by each chain is given by,

`\begin{gathered} F_h=Fcos\theta \\ =38.4* cos73.9\degree \\ =10.6\text{ N} \end{gathered}`

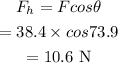
The vertical force by each chain is given by,

`\begin{gathered} F_v=Fsin\theta \\ =38.4* sin73.9\degree \\ =36.9\text{ N} \end{gathered}`

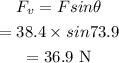
The weight of the light is balanced by the vertical force of the chains.

The weight of the light is,

`\begin{gathered} W=4F_v \\ =4*36.9 \\ =147.6\text{ N} \end{gathered}`

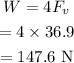
The mass of the light is,

`\begin{gathered} m=(W)/(g) \\ =(147.6)/(10) \\ =14.76\text{ kg} \end{gathered}`

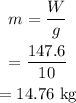
Hence, the mass of the light is 14.76 kg.