Given:
The is supported by four strong chains which make an angle of
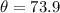
The force on each chain is
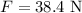
The acceleration due to gravity is
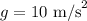
To find:
The mass of the light
Step-by-step explanation:
The horizontal force by each chain is given by,
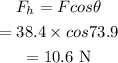
The vertical force by each chain is given by,
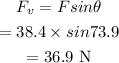
The weight of the light is balanced by the vertical force of the chains.
The weight of the light is,

The mass of the light is,
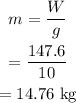
Hence, the mass of the light is 14.76 kg.