Question

What is the slope of the line that goes through (5, -1) and is perpendicular to a line with slope 2/5.

Answer 1

-5/2

Step-by-step explanation

Step 1

find the slope of the line :

when 2 lines are perpendicular the product of their slopes equals -1,so

`\begin{gathered} if\text{ line 1}\perp\text{ line 2} \\ then \\ slope_1*slope_2=-1 \end{gathered}`

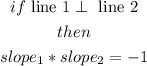
then, let

`\begin{gathered} slope_1=given=(2)/(5) \\ slope_2=slope_2 \\ hence \\ (2)/(5)*slope_2=-1 \\ to\text{ solve, multiply both sides by 5/2} \\ (2)/(5)slope_2*(5)/(2)=-1*(5)/(2) \\ slope_2=-(5)/(2) \end{gathered}`

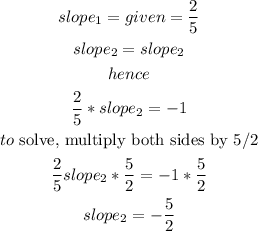
therefore, the slope of the line we are looking for is -5/2

Step 2

now, use the point-slope formula to find the equation of the line, it says

`\begin{gathered} y-y_1=m(x-x_1) \\ where\text{ m is the slope } \\ (x_1,y_1)\text{ is a point from the line} \end{gathered}`

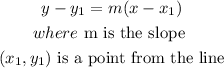
a)let

`\begin{gathered} slope=slope_2=-(5)/(2) \\ point=(5,-1) \end{gathered}`

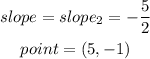
b) replace and solve for y to find the equation

`\begin{gathered} y-y_(1)=m(x-x_(1)) \\ y-(-1)=-(5)/(2)(x-5) \\ y+1=-(5)/(2)x+(25)/(2) \\ subtract\text{ 1 in both sides} \\ y+1-1=-(5)/(2)x+(25)/(2)-1 \\ y=-(5)/(2)x+(23)/(2) \end{gathered}`

therefore, the equation of the line is

`y=-(5)/(2)x+(23)/(2)`

and the slope is

`-(5)/(2)`

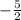
the slope of the line we are looking for is -5/2