-5/2
Step-by-step explanationStep 1
find the slope of the line :
when 2 lines are perpendicular the product of their slopes equals -1,so
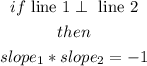
then, let
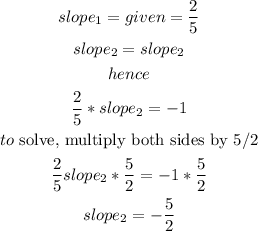
therefore, the slope of the line we are looking for is -5/2
Step 2
now, use the point-slope formula to find the equation of the line, it says
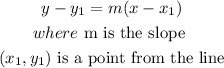
a)let
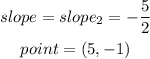
b) replace and solve for y to find the equation
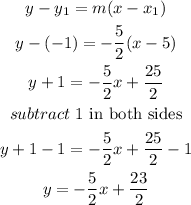
therefore, the equation of the line is
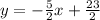
and the slope is
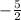
the slope of the line we are looking for is -5/2