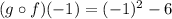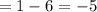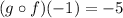Answer:
Given that,
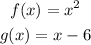
To find,a. (fog)(x)
b. (gof)(x)
c. (fog)( - 1)
d. (gof)( - 1)
we know that,
The composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h (x) = g (f (x)). It means here function g is applied to the function of x that is f(x).
It is represented as (gof)(x), i.e)
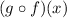
a)(fog)(x)
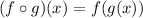
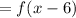
Put x=x-6 in the function f(x),
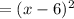
we get,
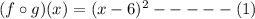
b)(gof)(x)
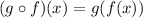
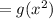
Put x=x^2 in the function g(x),
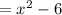
we get,
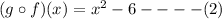
c) (fog)( - 1)
using equation (1), Put x=-1, we get
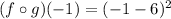
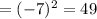
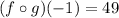
d) (gof)( - 1)
using the equation (2), Put x=-1, we get