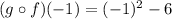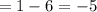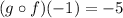Question

Let f(x) = x^2and g(x) = x – 6, find:a. (fog)(x) =b. (gof)(x) =c. (fog)( - 1) = d. (gof)( - 1) =

Answer 1

Given that,

`\begin{gathered} f(x)=x^2 \\ g(x)=x-6 \end{gathered}`

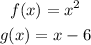
To find,a. (fog)(x)

b. (gof)(x)

c. (fog)( - 1)

d. (gof)( - 1)

we know that,

The composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h (x) = g (f (x)). It means here function g is applied to the function of x that is f(x).

It is represented as (gof)(x), i.e)

`(g\circ f)(x)`

a)(fog)(x)

`(f\circ g)(x)=f(g(x))`
`=f(x-6)`

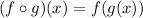
Put x=x-6 in the function f(x),

`=(x-6)^2`

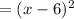
we get,

`(f\circ g)(x)=(x-6)^2-----(1)`

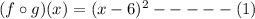
b)(gof)(x)

`(g\circ f)(x)=g(f(x))`
`=g(x^2)`

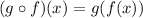
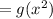
Put x=x^2 in the function g(x),

`=x^2-6`

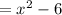
we get,

`(g\circ f)(x)=x^2-6----(2)`

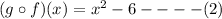
c) (fog)( - 1)

using equation (1), Put x=-1, we get

`(f\circ g)(-1)=(-1-6)^2`
`=(-7)^2=49`
`(f\circ g)(-1)=49`

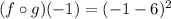
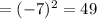
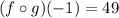
d) (gof)( - 1)

using the equation (2), Put x=-1, we get

`(g\circ f)(-1)=(-1)^2-6`
`=1-6=-5`

`(g\circ f)(-1)=-5`