Given the word problem, we can deduce the following information:
1. The radius r of a sphere is increasing at a rate of 4 inches per minute.
2. r =2 inches
To determine the change in volume, we first use the formula of the volume of sphere:
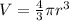
where:
V=Volume
r=radius
Next, we take the derivative of the volume:
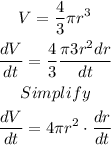
Hence,


We plug in r=2 and dr/dt=4 into the derivative of the volume of sphere:
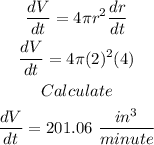
Therefore, the rate of change of the volume is 201.06 in^3/min.