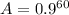Answer:
The value of A that makes the equation true is;
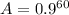
Step-by-step explanation:
We want to find the value of A that will make the equation below true;

Using the laws of indices we ca re-write the equation as;
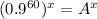
Then finding the xth root of both sides, we have;
![\begin{gathered} (0.9^(60))^x=A^x \\ \sqrt[x]{(0.9^(60))^x}=\sqrt[x]{A^x} \\ 0.9^(60)=A \\ A=0.9^(60) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mf7kbq29ap1xse0h1fpxuqxu4thrmgil4p.png)
Therefore, the value of A that makes the equation true is;