Question

How do I write 3+12+21+30+39+48using sigma notation

Answer 1

To answer this question, the (first) thing we need to find is the kind of sequence we have here. We can find this finding the common ratio (geometric sequence) or the common difference (arithmetic sequence).

We can prove that this is an arithmetic sequence since it has a common difference. If we subtract the second term of the sequence by the first term of the sequence, we have:

12 - 3 = 9

And,

21 -12 = 9

30 -21 = 9

And so on.

Therefore, we have an arithmetic sequence.

The arithmetic sequence will give us the expression to find the term in the sigma notation.

The arithmetic sequence is given (in general form) by:

`a_n=a_1+(n-1)d`

And we already know that:

a_1 = 3

d = 9

Then, we have:

`a_n=3+(n-1)\cdot9\Rightarrow a_n=3+9n-9\Rightarrow a_n=9n-6`

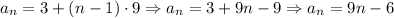
The latter is the general term of this arithmetic sequence. The sum of the first 6 elements of this arithmetic sequence is then:

In this way, we have that the first, second, third...and sixth term is given by this notation as follows:

And we have:

3 + 12 + 21 + 30 + 39 + 48

Hence, the sigma notation is as we drew above: