Right Triangle
If one of the interior angles of a triangle measures 90°, then we call the triangle a right triangle.
We must prove one of the angles formed by two of the sides of the triangle measures 90°. Those sides must be perpendicular to each other.
If two lines with slopes m1 and m2 are perpendicular, then:
m1 * m2 = -1
We'll calculate the slopes of each line defined by their endpoints (x1, y1) and (x2, y2) with the formula:

Calculate the slope of the segment ST:
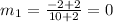
This represents a horizontal line.
Now for segment TR:
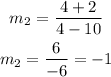
For segment SR:
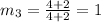
Note the product of m2 and m3 is -1, thus the triangle is right-angled at vertex R.