Question

Solving a percentage makes your problem using a system of linear equations

Answer 1

For the 1st fruit drink, 220 pints will be used

For the 2nd fruit drink, 40 pints will be used

Step-by-step explanation:

1st type has concentration = 35% = 0.35

2nd type has concentration = 100% = 1

let the amount for the 35% pure fruit = x

Total amount of fruit juice to be made = 260

amount for the 35% pure fruit + amount for the 100% pure fruit = 260

amount for the 100% pure fruit = 260 - x

concentration of mixture = 45% = 0.45

Amount = 260 pints

concentration for the 1st type (amount) + concentration of the 2nd type (amount) = concentration of mixture (amount)

`0.35(x)\text{ + 1}(260\text{ - x})\text{ = 0.45}(260)`

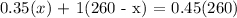
Solve for x:

`\begin{gathered} 0.35x\text{ + 260 - x = 117} \\ 0.35x\text{ - x + 260 = 117} \\ -0.65x\text{ + 260 = 117} \\ -0.65x\text{ = 117 - 260} \end{gathered}`
`\begin{gathered} -0.65x\text{ = - 143} \\ divide\text{ both sides by -0.65:} \\ (-0.65x)/(-0.65)\text{ = }(-143)/(-0.65) \\ x\text{ = 220} \\ \\ Amount\text{ for 35\% pure fruit = 220pints} \end{gathered}`

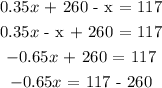
Amount for the 100% pure fruit = 260 - x

Amount for the 100% pure fruit = 260 - 220 = 40 pints

For the 1st fruit drink, 220 pints will be used and for the 2nd fruit drink, 40 pints will be used