Question

Indicate the maximum or minimum of value of f(x) whichever exists.

Answer 1

The given function is

`f(x)=x^2-2x-5`

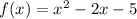
All quadratic functions represent a parabola. If the quadratic term is positive, the parabola opens up, if the quadratic term is negative, the parabola opens down.

In this case, we observe a positive quadratic term, so the parabola opens up, which means the function has a minimum.

To find the minimum of the function, we need to find its vertex (h,k), where

`h=-(b)/(2a)`

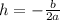
a = 1 and b = -2.

`h=-(-2)/(2(1))=(2)/(2)=1`

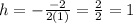
Then, evaluate the function to find k.

`f(1)=(1)^2-2(1)-5=1-2-5=1-7=-6`

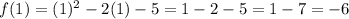
The k-coordinate of the vertex refers to the minimum value.

Therefore, the answer is -6.