Question

an alien on a distant planet realizes that using trigonometry and the distance to one of its moons it is possible to calculate the distance to the nearby son. Let 0 be the center of the planet and let A be the center of the Moon. the alien begins with the premise that during a Half Moon the Moon forms a right triangle with the sun and the planet by observing the angle between the Sun and Moon. theta equals 89.56 degrees and knowing the distance to the Moon is about 187000 km, estimate the distance from the planet to the Sun using these values. Round to the nearest 1000 km

Answer 1

Answer: 24351000 km

In order for us to find the distance from the planet to the sun, we first need to find the distance from the moon to the sun with the given values.

Let us first familiarize ourselves with SOH-CAH-TOA

`\sin \theta=(oppposite)/(hypotenus)`
`\cos \theta=(adjacent)/(hypotenuse)`
`\tan \theta=(opposite)/(adjacent)`

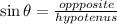
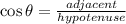
We are given an angle Ф of 89.56 and an adjacent angle of 187000.

In order to find the distance of the moon to the sun, which is the opposite of the given angle, we can use 'TOA' to solve for it.

`\tan \theta=(opposite)/(adjacent)`
`\tan 89.56=(opposite)/(187000)`
`opposite=(\tan 89.56)(187000)`
`=24350227.6055`

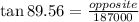
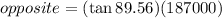
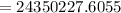
Now that we have the opposite distance of 24350227.6055 km, we can now find the distance from the planet to the sun by using the Pythagorean Theorem:

`c=\sqrt[]{a^2+b^2}`

Where:

c = distance from the planet to the sun

a = distance from the planet to the moon

b = distance from the moon to the sun

And since:

a = 187000

b = 24350227.6055

`c=\sqrt[]{187000^2+24350227.6055^2}`
`c=24350945.6375`

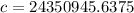
Rounding it off to its nearest 1000 km, it would be 24351000 km