We have a right triangle whose lengths are 26 inches and 36 inches.
We have that the largest side of a right triangle is the hypotenuse (c), and we can call the other side (one of the legs of the triangle) b. Then, using the Pythagorean Theorem, we have:
c = 36 inches.
b = 26 inches.
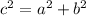
We can solve this equation for a^2, subtracting b^2 to both sides of the equation:
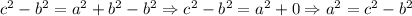
Then, we have:
![a^2=36^2-26^2\Rightarrow\sqrt[]{a^2}=\sqrt[]{1296-676}\Rightarrow a=\sqrt[]{620}\Rightarrow a=24.899799](https://img.qammunity.org/2023/formulas/mathematics/high-school/6u5ut68vnbfl8dckjzegl7sy6p9lj7i7m2.png)
Rounding this value to the nearest inch, we have that the value for a = 25 inches.