Question

Write the equation in slope-intercept form and then graph the equation that passes through (-4, -1) and is parallel to to y = −1/2x + 1

Answer 1

The general slope-intercept form of a linear equation is:

`y=mx+b`

----------------------------------------

You have a linear equation parallel to:

`y=-(1)/(2)x+1`

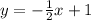
That means that both equations have the same slope

m= - 1/2

If the equation passes through (-4 , -1) we can use that point to find the value of the b in the slope-intercept form:

(-4 , -1) x= - 4 y= - 1

`-1=-(1)/(2)(-4)+b`

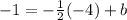
We clear the b:

`-1=(4)/(2)+b`
`-1=2+b`

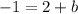
Then you know the values of

m=-1/2

b=-3

The equation in slope-intercept form is:

`y=-(1)/(2)x-3`

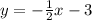
To graph a linear equation you need two point, as you have (-4, -1) and the point of the y-intercept that is (0,b) = (0,-3)

You put in the plane the two points:

And you draw a line that link the two points to get the final graph: