Question

On this problem, the answer has been worked out, but you must fill in the blanks in the solution.It is believed that 25% of U.S. homes have a direct satellite television receiver. How large a sample is necessary to estimate the true proportion of homes that do with 95% confidence and within 3 percentage points? How large a sample is necessary if nothing is known about the proportion?Solution: Notice that there are two questions, both about sample size for a proportion, so we use the formula

Answer 1

Step 1 :

We need to know how large a sample is necessary.

Let p denotes the United States Homes have a direct satellite TV Receiver is 25 % or 0. 25.

From the information, we know that E is 3 % or 0.03 and the confidence interval of 95%.

When p is known, then the sample size formula is :

`\begin{gathered} n\text{ = }^{}\frac{\lbrack Z_{(\alpha)/(2)}\rbrack^2}{E^2}\text{ X p x q} \\ \text{where p + q = 1} \end{gathered}`

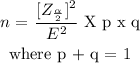
When p is unknown, then the sample size formula is:

`n\text{ = }\frac{\lbrack Z_{(\propto)/(2)}\rbrack^2}{E}\text{ X 0.25}`

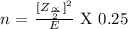
Now, we have to determine:

`Z_{(\alpha)/(2)}`

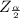
The confidence level is :

`1\text{ - }\alpha`

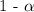
We know that:

`\begin{gathered} \alpha\text{ = 95\% = 0.95} \\ 1\text{ - }\alpha\text{ = 1 - 0.95} \\ \text{1 - }\alpha\text{ = 0.05} \\ Z_{(\alpha)/(2)\text{ }}=\text{ 0.05/ 2} \end{gathered}`
`Z_{(0.05)/(2)\text{ }}=\text{ 1.96 ( using table value )}`

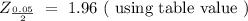
If we use the known p, then the sample size is :

`\begin{gathered} n\text{ = }((1.96)^2)/((0.03)^2)\text{ X ( 0.25 ) ( 0.75 )} \\ n\text{ = }(3.8416)/(0.0009)\text{ x 0.1875} \\ \text{n = 4268.44444 x 0.1875} \\ n\text{ = 800.333} \\ n\text{ }\approx\text{ 801} \end{gathered}`

If we use the known p, then the sample size is 801.

Therefore, a sample n is 801.

Step 2 :

If we use the un-known p , then the sample size is :

`\begin{gathered} n\text{ = }((1.96)^2)/((0.03)^2)\text{ x 0. 25} \\ \text{n = }(3.8416)/(0.0009)\text{ x 0.25} \\ n\text{ = 4268.44444 x 0.25} \\ \text{n = 1067. 11111} \\ n\approx\text{ 1068} \end{gathered}`

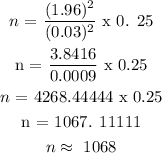
If we use the unknown p, then the sample size is approximately 1068.

Therefore, a sample n is 1068.