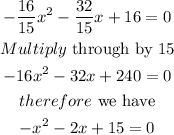To find the solution to the question we would use the general representation of a quadratic equation below:
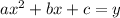
We then pick a suitable point
When x=0 and y =16
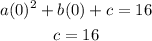
We then pick two more suitable points, then solve the resulting simultaneous equation
When x= 3 and y= 0
we have
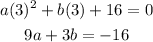
Also, when x=-5 and y =0
we have
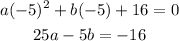
We have gotten two equations, we will solve them simultaneously using the elimination method.
We will multiply equation one by 5 and equation two by 3
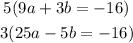
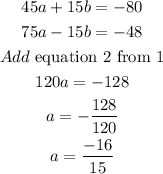
Substitute the value of a in equation 1
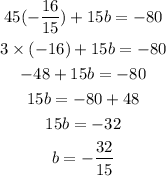
We will then substitute a and b and c in the representation of the quadratic equation.