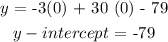Question

9) Write the equation of the parabola with vertex ( 5,-4) and concavity-3, determine whether the parabola is concave up or concave down and find the y-intercept:

Answer 1

The equation of a parabola in vertex form is given by

`f(x)=a(x-h)^2\text{ + k}`

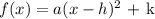
The vertex (h,k) when compared with the equation, h = 5 and k = -4

Since the concavity is -3,

a= -3

`y=-3(x-5)^2\text{ + (-4)}`

`\begin{gathered} y=-3(x-5)^2\text{ -4} \\ y=-3(x^2-10x+25\text{) - 4} \\ y=-3x^2\text{ + 30x -75 -4} \\ y=-3x^2\text{ + 30x -79} \end{gathered}`

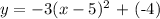
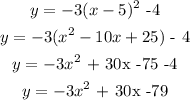
From the graph shown, it can be seen that the parabolic curve is concave down

To get the y-intercept

we will have to put x = 0 into the equation

`\begin{gathered} y\text{ = -3(0) + 30 (0) - 79} \\ y-intercept\text{ = -79} \end{gathered}`