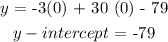The equation of a parabola in vertex form is given by
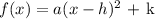
The vertex (h,k) when compared with the equation, h = 5 and k = -4
Since the concavity is -3,
a= -3
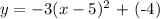
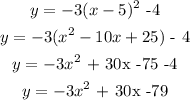
From the graph shown, it can be seen that the parabolic curve is concave down
To get the y-intercept
we will have to put x = 0 into the equation