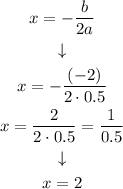Axis of symmetry of a quadratic equation
We know that for an equation of the form:

the axis of symmetry is given by:

In this case, where our formula is given by the equation:
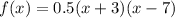
we want to multiply all the factors so we can work with the form of the first equation. We do this using the distributive property:
0.5 (x + 3) = 0.5 · x + 0.5 · 3
= 0.5x + 1.5
Then, in the equation:
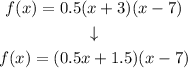
Now, multiplying both (0.5x + 1.5) and (x - 7) we have that:
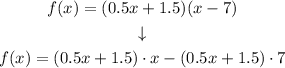
Now, finding the product of
(0.5x + 1.5)x, we have that:
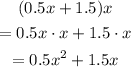
Replacing in the equation:
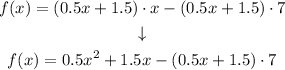
On the other hand, finding the product of
-(0.5x + 1.5) · 7,we have that
-(0.5x + 1.5) · 7 = -0.5x · 7 - 1.5 · 7
= -3.5x - 10.5
Replacing in the equation:
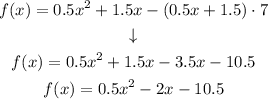
Then, we have that
a = 0.5,
b = -2
and
c = -10.5
Then, using the equation for the axis of symmetry, we have that: