Given the functions f(x) and g(x) defined as:
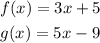
(a)
We use the definition of the addition of two functions:
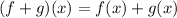
Then:
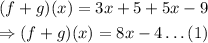
This is a polynomial, so the domain is x
(b)
Using the definition of subtraction of two functions:
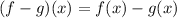
Then:
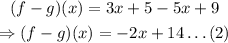
This is a polynomial, so the domain is x is any real number
(c)
We use the definition of the product between two functions:
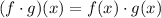
Then:
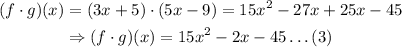
This is a polynomial, so the domain is x is any real number
(d)
We use the definition of the quotient between two functions:
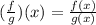
Then:
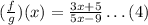
This is a rational expression, so the domain is the set of all the numbers such that the denominator is not 0. Finding those values:
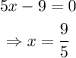
The domain is x
(