Question

I need help with this problem from the calculus portion on my ACT prep guide

Answer 1

Given a series, the ratio test implies finding the following limit:

`\lim _(n\to\infty)\lvert(a_(n+1))/(a_n)\rvert=r`

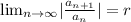
If r<1 then the series converges, if r>1 the series diverges and if r=1 the test is inconclusive and we can't assure if the series converges or diverges. So let's see the terms in this limit:

`\begin{gathered} a_n=(2^n)/(n5^(n+1)) \\ a_(n+1)=(2^(n+1))/((n+1)5^(n+2)) \end{gathered}`

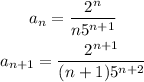
Then the limit is:

`\lim _(n\to\infty)\lvert(a_(n+1))/(a_n)\rvert=\lim _(n\to\infty)\lvert(n5^(n+1))/(2^n)\cdot(2^(n+1))/(\mleft(n+1\mright)5^(n+2))\rvert=\lim _(n\to\infty)\lvert(2^(n+1))/(2^n)\cdot(n)/(n+1)\cdot(5^(n+1))/(5^(n+2))\rvert`

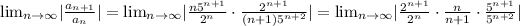
We can simplify the expressions inside the absolute value:

`\begin{gathered} \lim _(n\to\infty)\lvert(2^(n+1))/(2^n)\cdot(n)/(n+1)\cdot(5^(n+1))/(5^(n+2))\rvert=\lim _(n\to\infty)\lvert(2^n\cdot2)/(2^n)\cdot(n)/(n+1)\cdot(5^n\cdot5)/(5^n\cdot5\cdot5)\rvert \\ \lim _(n\to\infty)\lvert(2^n\cdot2)/(2^n)\cdot(n)/(n+1)\cdot(5^n\cdot5)/(5^n\cdot5\cdot5)\rvert=\lim _(n\to\infty)\lvert2\cdot(n)/(n+1)\cdot(1)/(5)\rvert \\ \lim _(n\to\infty)\lvert2\cdot(n)/(n+1)\cdot(1)/(5)\rvert=\lim _(n\to\infty)\lvert(2)/(5)\cdot(n)/(n+1)\rvert \end{gathered}`

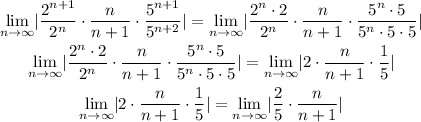
Since none of the terms inside the absolute value can be negative we can write this with out it:

`\lim _(n\to\infty)\lvert(2)/(5)\cdot(n)/(n+1)\rvert=\lim _(n\to\infty)(2)/(5)\cdot(n)/(n+1)`

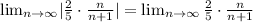
Now let's re-writte n/(n+1):

`(n)/(n+1)=(n)/(n\cdot(1+(1)/(n)))=(1)/(1+(1)/(n))`

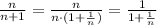
Then the limit we have to find is:

`\lim _(n\to\infty)(2)/(5)\cdot(n)/(n+1)=\lim _(n\to\infty)(2)/(5)\cdot(1)/(1+(1)/(n))`

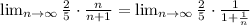
Note that the limit of 1/n when n tends to infinite is 0 so we get:

`\lim _(n\to\infty)(2)/(5)\cdot(1)/(1+(1)/(n))=(2)/(5)\cdot(1)/(1+0)=(2)/(5)=0.4`

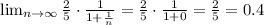
So from the test ratio r=0.4 and the series converges. Then the answer is the second option.