We have the following equation for the amount in grams of radiactive isotope:
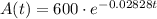
where t denotes the time in years.
a. Find the initial amount of the isotope that is present in the sample.
The initial amount of the isotope occurs at t=0. Then, by substituting this value into to our equation, we have
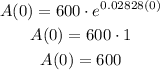
Then, the initial amount is 600 grams.
b. Find the half-life of this isotope.
In this case, the final amount must be half of the starting material, that is,
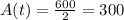
and the half-life is the corresponding time for this amount of material. So, we have
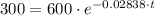
By moving 600 to the left hand side, we get
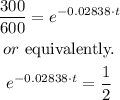
therefore, the time is given as
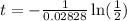
then, the time is

then. by rounding down, the answer is 24 years.