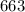Given:
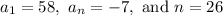
Required:
We have to find the arithmetic series.
Step-by-step explanation:
From the given data if we can find the common difference denoted by d then we can easily find the required arithmetic series.
We use the formula

Now we put the given values in the above equation to find the value of d.
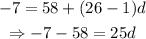
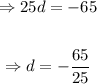
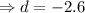
Then the required arithmetic series is
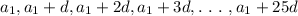
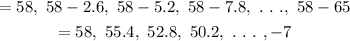
The formula for finding the sum of the arithmetic series is

Then the sum of the above series is
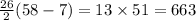
Final answer:
Hence the arithmetic series is
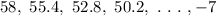
And the sum of the series is