Answer:
The ball hits the ground at t = 8 seconds
The ball is at its maximum height of 25 m at t = 3 seconds
Step-by-step explanation:
The expression that model the height of the ball after t minutes is:
H(t) = -t² + 6t + 16
The ball hits the ground when its height is 0, so we need to solve the following equation:
-t² + 6t + 16 = 0
If we multiply this equation by -1, we get an equivalent expression:
t² - 6t - 16 = 0
To factorize, we need to find two numbers that sum to -6 and that multiply to -16. These numbers are -8 and 2, therefore:
(t - 8)(t + 2) = 0
Solving for t, we get:
t - 8 = 0
t - 8 + 8 = 0 + 8
t = 8
or
t + 2 = 0
t + 2 - 2 = 0 - 2
t = -2
Since t = -2 doesn't have sense here. The ball hits the ground after 8 seconds,
On the other hand, the maximum height is found in the vertex of the parabola. So, the first coordinate for the vertex is equal to:
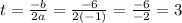
because b is the coefficient beside t and a is the coefficient besides t².
Now, we can replace t = 3 on the equation to find h(t)
H(t) = -t² + 6t + 16
H(t) = -3² + 6(3) + 16
H(t) = -9 + 18 + 16
H(t) = 25
Therefore, the answers are:
The ball hits the ground at t = 8 seconds
The ball is at its maximum height of 25 m at t = 3 seconds