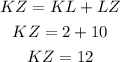Question

Chords WP and KZ intersect at point L in the circle shown.Wzr3.x - 22LK5РWhat is the length of KZ?7.5910O 12

Answer 1

If the chords intersect inside the circle, the product of the lengths of the segments of the chords are equal.

`(KL)(LZ)=(WL)(LP)`

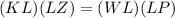
Substitute the given values into the equation and then solve for the value of x.

`\begin{gathered} 2(3x-2)=x(5) \\ 6x-4=5x \\ 6x-5x=4 \\ x=4 \end{gathered}`

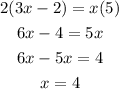
Since the value of KZ is the sum of the length of KL and LZ, we must find the length of LZ. Substitute the value of x into the expression and then simplify.

`\begin{gathered} LZ=3x-2 \\ =3(4)-2 \\ =12-2 \\ =10 \end{gathered}`

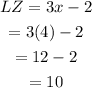
To obtain the value of KZ, add the lengths of KL and LZ.

`\begin{gathered} KZ=KL+LZ \\ KZ=2+10 \\ KZ=12 \end{gathered}`