Answer:
10.61 m/s
Step-by-step explanation:
To find the final speed, we will use the conservation of momentum in each direction, so we can write the following equations:
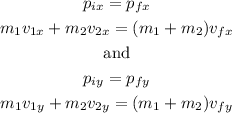
Where m1 and m2 are the mass of the vehicles, v1 and v2 are their respective velocities in each direction, and Vfx and Vfy are the final velocities in each direction.
If one of the vehicles is headed north, its horizontal velocity Vx = 0 m/s. In the same way if the other is headed east, its vertical velocity Vy = 0m/s
Therefore, we can replace the values and solve the first equation as:
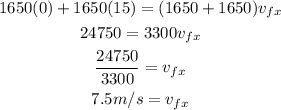
In the same way, we can solve the second equation as:
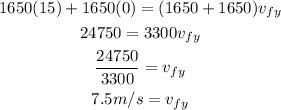
Now, we know that the vertical and horizontal speed was 7.5 m/s. So, we can calculate the final speed using the Pythagorean theorem as:
![\begin{gathered} v=\sqrt[]{(v_(fx))^2+(v_(fy))^2} \\ v=\sqrt[]{(7.5)^2+(7.5)^2} \\ v=\sqrt[]{56.25+56.25} \\ v=\sqrt[]{112.5}=10.61\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/q7z3pyt36h1r4mza9voxs9o3d5xohhjwob.png)
So, the speed after the collision was 10.61 m/s