Question

A wave is modeled with the function y = 1/2 sin (3Θ) , where Θ is in radians. Describe the graph of this function, including its period, amplitude, and points of intersection with the x-axis.

Answer 1

`y=Asin\left(B\theta\right)`

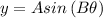
In the function above:

A is the amplitude

2π/B is the period

You equal to 0 the function and solve θ to find the points of intersection with the x-axis.

For the given function:

`y=(1)/(2)sin\left(3\theta\right)`

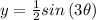
Amplitude:

`A=(1)/(2)`

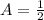
Period:

`P=(2\pi)/(3)`

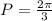
Points of intersection with the x-axis:

`\begin{gathered} (1)/(2)sin\left(3\theta\right)=0 \\ \\ Multiply\text{ both sides of the equatio by 2:} \\ 2*(1)/(2)sin\left(3\theta\right)=2*0 \\ \\ sin\left(3\theta\right)=0 \end{gathered}`

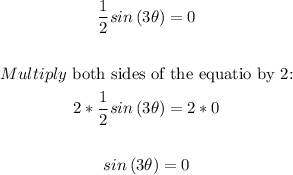
Using the unit circle you get that the angles with sine equal to 0 are: 0 and π.

`\begin{gathered} 3\theta=0 \\ 3\theta=\pi \end{gathered}`

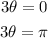
Solve θ:

`\begin{gathered} \theta=0 \\ \\ \theta=(\pi)/(3) \end{gathered}`

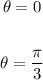
Add the period to each solution multiplied by k of θ to find all the intersections:

`\begin{gathered} \theta=0+(2k\pi)/(3) \\ \\ \theta=(\pi)/(3)+(2k\pi)/(3) \end{gathered}`

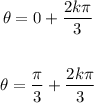
Combine the solutions:

`\theta=(k\pi)/(3)`

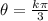
Then, the given function has Amplitude 1/2; period 2π/3, and points of intersection kπ/3 (k is a whole number)