Question

The following equation is given.x4 + 6x3 + 6x2 + 6x +5=0a. List all possible rational roots.b. Use synthetic division to test the possible rational roots and find an actual root.Actual rational root: c. Use the root from part (b.) and solve the equation.The solution set of x4 + 6x2 + 6x2 + 6x + 5 = 0

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

x^4 + 6x^3 + 6x^2 + 6x +5=0

roots = ?

Step 02:

a. possible rational roots

rational root theorem:

possible rational roots = factors of the constant / factors of the lead

x^4 + 6x^3 + 6x^2 + 6x + 5=0

lead = 1

constant = 5

factors of the coefficient, 1 are ±1

factors of the constant term, 5 are ±1 , ±5

possible rational roots = (±1 , ±5) / ±1

possible rational roots = ±1 , ±5

Step 03:

b. synthetic division

possible rational root:

(x + 1) ===> x = - 1

-1 | 1 6 6 6 5

| -1 -5 -1 - 5

------------------------------

1 5 1 5 0

The remainder is 0

Step 04:

c. solve the equation

x = -1

x^4 + 6x^3 + 6x^2 + 6x + 5 = 0

`\begin{gathered} (-1)^4+6(-1)^3+6(-1)^2+6(-1)+5=0 \\ 1\text{ - 6 + 6 - 6 + 5 = 0} \\ 0\text{ = 0 } \end{gathered}`

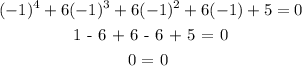
That is the full solution.