Question

Provide the missing statement and reasons for the following proof:Given: 9(2 – 6) +41 = 75Prove: I=889ReasonStatement$1 9(x-6) + 41 - 75R1S2. 9(x - 6) - 34R2.S3| |R3 Distributive PropertyS4 9x = 88R488S5 * -R5

Answer 1

Given:

`9(x-6)+41=75`

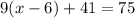
Step-by-step explanation:

Solve the equation to obtain the value of x.

`9(x-6)+41=75\text{ (Given)}`

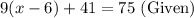
Substract 41 from both sides of equation.

`9(x-6)+41-41=75-41\text{ (Substract 41 from both sides)}`

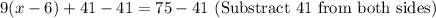
Apply distributive property .

`9\cdot x-9\cdot6=34\text{ (Distributive property)}`

Add 54 to both sides of equation.

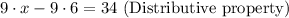
`9x-54+54=34+54\text{ (Add 54 to both sides of equation)}`

Divide both sides of equation by 9.

`\begin{gathered} (9x)/(9)=(88)/(9) \\ x=(88)/(9)\text{ (Divide both sides by 9)} \end{gathered}`

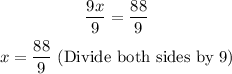
Answers:

R1: Given

R2: Subtract 41 from both sides of equation (Subtractiove property of equality)

S3: 9*x -9*6 = 34

R4: Add 54 to both sides of equation (Additive property of equality)

R5: Divide both sides of equation by 9 (Division property of equality)