Given:
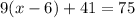
Step-by-step explanation:
Solve the equation to obtain the value of x.
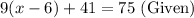
Substract 41 from both sides of equation.
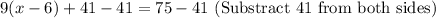
Apply distributive property .
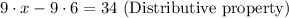
Add 54 to both sides of equation.

Divide both sides of equation by 9.
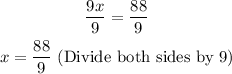
Answers:
R1: Given
R2: Subtract 41 from both sides of equation (Subtractiove property of equality)
S3: 9*x -9*6 = 34
R4: Add 54 to both sides of equation (Additive property of equality)
R5: Divide both sides of equation by 9 (Division property of equality)