Question

Which equation represents a line perpendicular to line WX shown? a) y=2x+4b) y=-5/3x+8c) y=-9-2xd) y=1/2x+6

Answer 1

First, we have to find the slope of the given line.

We use the following formula to find the slope.

`m=(y_2-y_1)/(x_2-x_1)`

Let's replace the points (-3, -4) and (5, 0) in the formula.

`m=(0-(-4))/(5-(-3))=(4)/(5+3)=(4)/(8)=(1)/(2)`

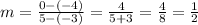
The slope of the given line is 1/2.

Now, we find the slope of the new perpendicular line with the following formula.

`\begin{gathered} m\cdot m_1=-1 \\ m\cdot(1)/(2)=-1 \\ m=-2 \end{gathered}`

The slope of the given perpendicular line is -2.

Notice that C is the only equation that has a slope of -2 because the coefficient of x is -2.

Therefore, the answer is C.