Question

Consider the following function.f(x) = cos 9x2 Find the derivative of the function.

Answer 1

The given function is:

`f(x)=\cos((9x)/(2))`

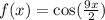
It is required to find the derivative of the function and then use it to determine if the function is strictly monotonic, and hence has an inverse.

First, find the derivative of the function:

`\begin{gathered} f(x)=\cos((9x)/(2)) \\ Take\text{ derivative of both sides:} \\ f^(\prime)(x)=(d)/(dx)\cos((9x)/(2)) \\ Using\text{ the chain rule }f^(\prime)(g(x))=(d)/(df)(f)*(d)/(dx)(g(x))\text{, the derivative is:} \\ f^(\prime)(x)=-\sin((9x)/(2))*(d)/(dx)((9x)/(2))=-(9)/(2)\sin((9x)/(2)) \\ \Rightarrow f^(\prime)(x)=-(9)/(2)\sin((9x)/(2)) \end{gathered}`

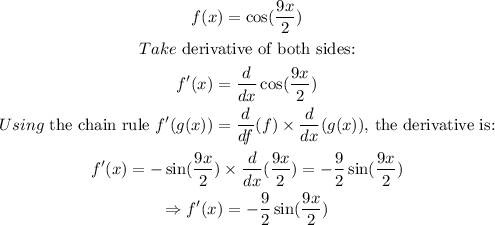
Notice that the derivative of the function is a trigonometric function that is sinusoidal (alternates in values from negative to positive).

A function is strictly monotonic if its derivative is strictly positive or strictly negative over its entire domain.

Hence, the given function is not strictly monotonic and therefore does not have an inverse.

Answers:

The derivative of the function is:

`f^(\prime)(x)=-(9)/(2)\sin((9x)/(2))`

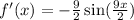
The given function is not strictly monotonic and therefore does not have an inverse.