Question

Try some examples with 3 odd numbers to check this conjecture

Answer 1

We have the following conjecture: "The square of an odd number is always odd".

4.1) We select the odd numbers 1, 3, 5 and check the conjecture:

`\begin{gathered} 1^2=1, \\ 3^2=9, \\ 5^2=25. \end{gathered}`

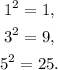
We notice that the results of the squares are odd numbers, so the conjecture is true for these numbers.

4.2) We can't find an example where the conjecture is false. In point 4.4, we will prove that the conjecture is true.

4.3) We agree with the conjecture. We believe that it is TRUE.

4.4) We prove that the conjecture is true for all odd numbers.

By definition, an odd number can be written as:

`m=2n+1.`

Where:

• n is an integer,

,

• 2n is an even number because 2n is divisible by 2.

Now, we compute the square of m:

`m^2=(2n+1)^2=(2n+1)\cdot(2n+1)=4n^2+4n+1=2\cdot(2n^2+2n)+1.`

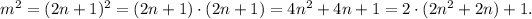
We see that the result is the sum of an even number 2*(2n²+2n) plus 1, so the result is an odd number for every odd number m = 2n + 1. This result proves the conjecture.

The conjecture is TRUE for all odd numbers.