Question

Is this figure defined W,X,Y and Z a rhombus? justify your answer

Answer 1

Step 1: Write out the formula for finding the distance d between two points (x1,y1) and (x2,y2)

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \end{gathered}`

Step 2: Find the distance between the vertices of the figure

The distance d1 between vertices X(6,-5) and Y(11,-5) is 11-6 = 5 units.

The distance d2 between vertices Y(11,-5) and Z(11,-10) is -5 -- 10 = 5 units.

The distance d3 between vertices Z(11,-10) and W(6,-10) is 11 - 6 = 5 units.

The distance d4 between vertices W(6,-10) and X(6,-5) is -5 -- 10 = 5 units.

Hence all the sides of the figure are congruent

Step 3: Write out the formula for finding the gradient m of the line joining two points (x1,y1) and (x2,y2).

`m=(y_2-y_1)/(x_2-x_1)`

Step 4: Check if side XY is Parallel to side WZ

Let m1 be the gradient of XY. Then

`m1=(-5--5)/(11-6)=(0)/(5)=0_{}`

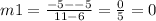
Let m2 be the gradient of WZ. Then

`m2=(-10--10)/(11-6)=(0)/(5)=0_{}`

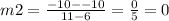
Hence XY is parallel to WZ ( and they are parallel to the x-axis)

Step 5: Check if side XW is Parallel to side YZ

Let m1 be the gradient of XW. Then

Let m2 be the gradient of YZ. Then

Hence XY is parallel to YZ ( and they are parallel to the y-axis)

Therefore,

WXYZ is a rhombus. Based on the coordinates opposite sides are parallel and all the sides are congruent

The second option