Solution:
The intermediate value theorem for polynomials states that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis.
To prove it has a real zero, it must cross the x-axis.
The theorem thus states mathematically that;
![\begin{gathered} f(a)<strong>Given:</strong>[tex]\begin{gathered} a=-1 \\ b=0 \\ f(x)=-8x^5+5x^3-6x^2+1 \end{gathered}]()
We test for the continuity of the polynomial at x = a and x = b
Hence,
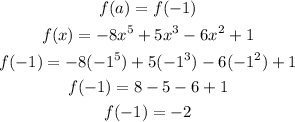
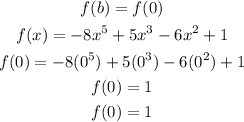
From the above, since the value of the output of the function at the input (intervals) -1 and 0 changes from negative to positive (i.e, from -2 to 1), then it should pass through the x-axis.
Once the function passes through the x-axis, then it will have a real zero between the interval given.